This week on RCloud: https://rstudio.cloud/project/1156832



Datasets for this class:

A random sample of 1,000 federal personnel records for March 1994:



library(dplyr)
library(ggplot2)

Load Dataset

load("Datasets/OPM94.RData")


Confidence Interval for a Population Mean Calculated Manually (mean edyrs)

Sample mean:

x_bar <- mean(opm94$edyrs, na.rm = TRUE)
x_bar
## [1] 14.366

Sample standard deviation:

sd_x <- sd(opm94$edyrs, na.rm = TRUE)
sd_x
## [1] 2.263441

Standard error (standard deviation of the sample mean/of the sampling distribution for the sample mean):

se <- sd_x/sqrt(1000)
se
## [1] 0.0715763

The critical value of the t-statistic for 95% confidence level: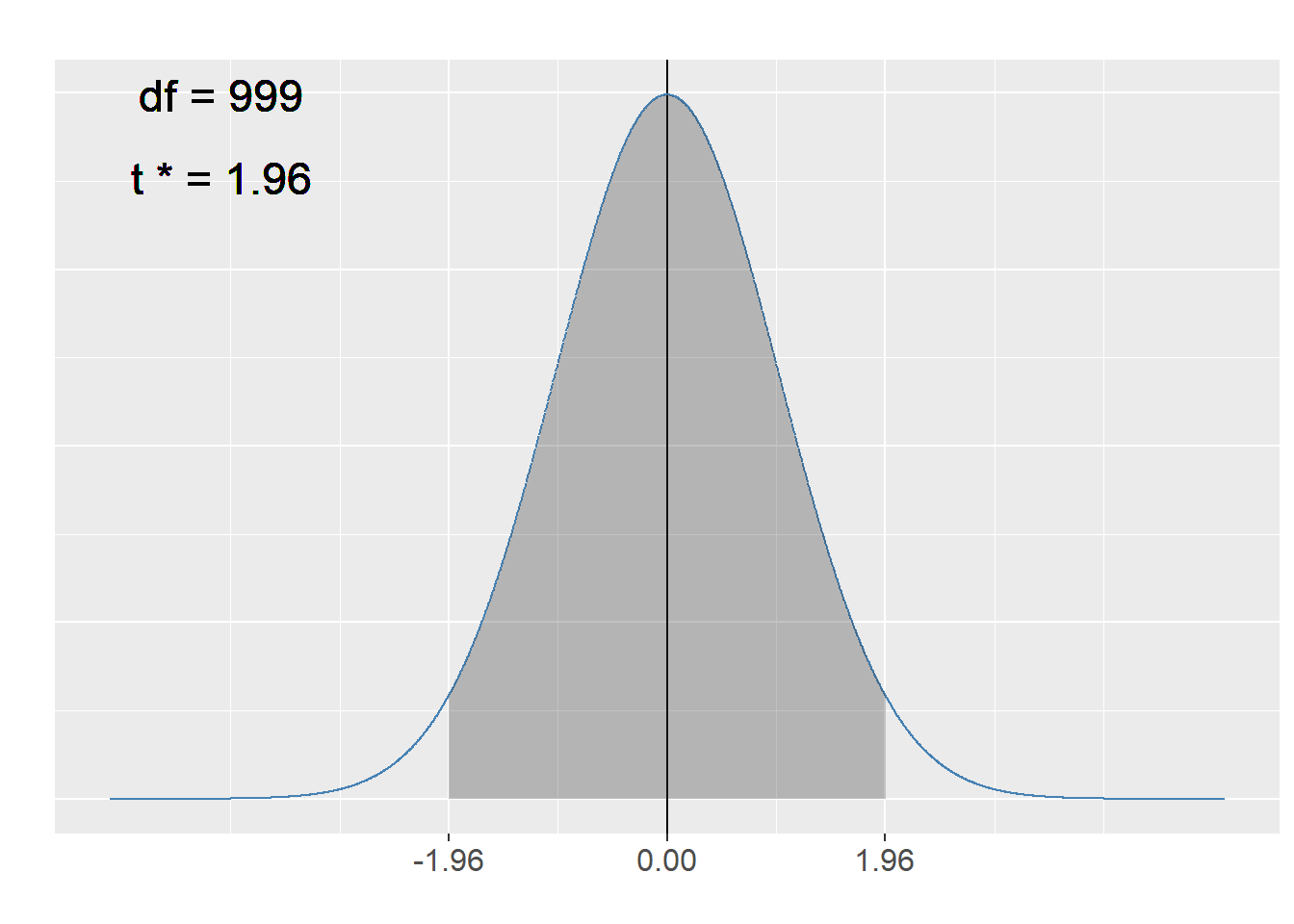

The shaded area represent 95% of the total area under the t-distribution. Each of the tail areas are 2.5% of the total area. To find the critical value of t* for that interval, we need to find a t value corresponding either 0.975 (97.5%) of the distribution in the lower tail or 0.025 (2.5%) of the distribution in the upper tail.

Calculation of the critical value t* using qt() function:

t <- qt(p = 0.975, df = 999, lower.tail = TRUE)    # 97.5% of the distribution in the lower tail 
t
## [1] 1.962341
t <- qt(p = 0.025, df = 999, lower.tail = FALSE)   # 2.5% of the distribution in the upper tail  
t
## [1] 1.962341

You can also find the critical value of t* using the visual applet at https://yuriygdv.github.io/pmap4041spring2020/app-t-distr.html

95% confidence interval for the mean years of education edyrs in the population of federal employees:

x_bar - t*se      # lower bound
## [1] 14.22554
x_bar + t*se      # upper bound
## [1] 14.50646


Conclusion:

We are 95% confident that in the population of federal employees in 1994, the mean value of years of education was between 14.2255429 and 14.5064571


Confidence Interval Using t.test

We can run a t-test and obtain the same confidence interval using t.test() function:

t.test(opm94$edyrs, conf.level = 0.95)
## 
##  One Sample t-test
## 
## data:  opm94$edyrs
## t = 200.71, df = 999, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  14.22554 14.50646
## sample estimates:
## mean of x 
##    14.366

Conclusion:

As we can see in the output, the 95 percent confidence interval is 14.22554 to 14.50646, which corresponds the results calculated manually.


Is the mean number of years of education in the population of federal employees different from 14?

Let’s run a t-test specifying the value of μ described in H0:

t.test(opm94$edyrs, mu = 14, conf.level = 0.95  )
## 
##  One Sample t-test
## 
## data:  opm94$edyrs
## t = 5.1134, df = 999, p-value = 3.791e-07
## alternative hypothesis: true mean is not equal to 14
## 95 percent confidence interval:
##  14.22554 14.50646
## sample estimates:
## mean of x 
##    14.366

Conclusion:

Yes, because t is greater than the critical value of 1.96 (and p-value is less than 0.05), we can reject the null hypothesis that the mean `edyrs` in the population equals 14. Hence, we can be 95% confident that it's different from 14 in the population of federal employees.


Is the mean number of years of education in the population of federal employees greater than 14?

Let’s run a t-test specifying the value of μ described in H0 and the type of alternative hypothesis:

t.test(opm94$edyrs, mu = 14, alternative = "greater", conf.level = 0.95  )
## 
##  One Sample t-test
## 
## data:  opm94$edyrs
## t = 5.1134, df = 999, p-value = 1.896e-07
## alternative hypothesis: true mean is greater than 14
## 95 percent confidence interval:
##  14.24816      Inf
## sample estimates:
## mean of x 
##    14.366

Conclusion:

Yes, because the t-statistic is greater than the critical value of 1.96 (and p-value is less than 0.05), we can reject the null hypothesis that the mean `edyrs` in the population is less or equal to 14. Hence, we can be 95% confident that the mean `edyrs` in the population of federal employees is greater than 14.


Is the mean number of years of education in the population of federal employees different from 14.5?

Let’s run a t-test specifying the value of μ described in H0:

t.test(opm94$edyrs, mu = 14.5, conf.level = 0.95  )
## 
##  One Sample t-test
## 
## data:  opm94$edyrs
## t = -1.8721, df = 999, p-value = 0.06148
## alternative hypothesis: true mean is not equal to 14.5
## 95 percent confidence interval:
##  14.22554 14.50646
## sample estimates:
## mean of x 
##    14.366

Conclusion:

No, because the t-statistic is lower than the critical value of 1.96 (and p-value is greater than 0.05), we cannot reject the null hypothesis that the true mean `edyrs` in the population is different from 14.5. Hence, we tentatively accept the null hypothesis.


Does the mean salary of veterans differ from the mean salary of those who don’t receive veteran preferences in the population of federal employees?

Let’s run a t-test specifying the the outcome vaiable sal and the factor/categorical variable to test the difference for:

t.test(sal ~ vet, data = opm94)
## 
##  Welch Two Sample t-test
## 
## data:  sal by vet
## t = -4.0401, df = 353.15, p-value = 6.559e-05
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -8429.905 -2909.792
## sample estimates:
##  mean in group no mean in group yes 
##          39439.66          45109.51

Conclusion:

In the t-test output, we can see that t = -4.04 (the absolute value of the t-statistic is greater than 1.96) and p-value = 6.559e-05 (= 0.00006559), which is much smaller than our conventional significance level of alpha = 0.05, which implies that if in the population of federal employees the difference in mean salaries of veterans and nonveterans was equal 0, obtaining the t-statistics of 4.04 or larger would be extremely unlikely. This provides us with evidence that the difference in salaries in the population is not equal to zero. In other words, the difference in the mean salary is statistically significantly different from zero in the population of federal employees.

According to the confidence interval, we can be 95 percent confident that veterans in the federal government receive a mean salary that is $2,909 to $8,429 higher than the mean salary of nonveterans.